Excel : créer des binômes à partir de 3 listes

[NinaB]

Bonjour,

Étant enseignante je participe à un projet avec deux autres collègues.
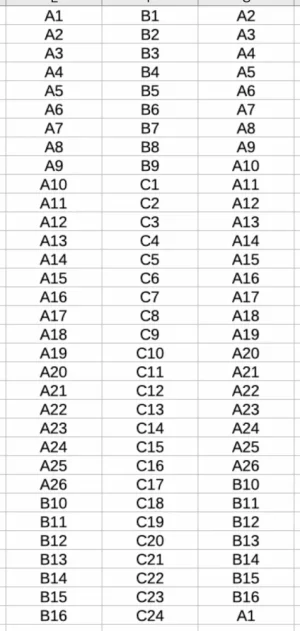
J'ai besoin de mettre les élèves de nos 3 classes par deux, tout en veillant à ne pas mettre deux élèves de la même classe ensemble.

Pour l'instant je n'ai réussi qu'à tirer au sort les élèves mais je n'arrive pas à faire en sorte que deux élèves de la même classe ne soient pas ensemble...

Pouvez-vous m'aider s'il vous plait ? Ma demande est assez urgente...

Merci d'avance !!

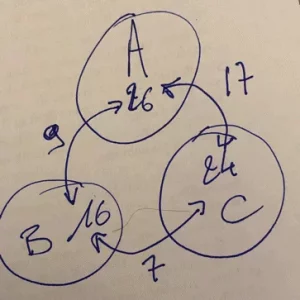
(Admettons nos trois classes A, B et C, ayant respectivement 26, 16 et 24 élèves, ce qui donne 66 élèves. Je dois donc constituer 66 binômes car chaque enfant doit envoyer quelque chose à quelqu'un, c'est pour une correspondance entre classes)

 

[radioman]

Hum: 66 élèves ça fait 33 binômes …
9 binômes A<->B (16-9 restes 7 élèves B)
17 binômes A<->C (24-7 restes 7 élèves C)
17+9 élèves A : tout le monde A est casé
du coup faire 7 binômes B<->C … tout le monde B et C est casé, on a bien nos 33 binômes .

 

[radioman]

edit: faute de frappe: il faut lire 17 binômes A<->C (24-17 restes 7 élèves C)

Edit 2:
Mon fils s’est amusé à trouver la formule de calcul :

soit 3 établissements A,B,C avec X,Y,Z élèves (X≥Y≥Z) et X+Y+Z est pair

X = a+b (et Y≥a , Z≥b )
Y-a = Z-b

donc a=(X-Z+Y)/2 et b=(X-Y+Z)/2

 

[radioman]

​

 

[Aliboron]

C'est faisable (péniblement) dans Excel avec une macro. Mais tu as meilleur compte à faire simple, la solution qu'indique radioman juste ci-dessus (il m'a grillé sur le fil ! ) : appairer les 9 premiers du groupe B avec des élèves du groupe A et les sept suivants avec des élèves du groupe C. Reste ensuite à appairer les 17 restants des groupes A et C...

 

[radioman]

en entrant les formules dans excel ça doit marcher …

 

[NinaB]

Merci pour vos réponses ! Je n'ai pas reçu de mail je viens seulement de les voir...

Cependant je dois bien constituer 66 binômes et non 33 : en effet, les 66 élèves doivent envoyer une lettre à un seule élève.
C'est à dire que l'élève A doit envoyer une lettre à B et l'élève B doit envoyer une lettre à C, ainsi de suite...

En gros, j'aimerais attribuer un élève aux 66 élèves, mais en faisant attention que deux élèves de la même classe ne se retrouvent pas ensemble...

Je voulais donc savoir si il y avait un moyen de le faire par Excel à l'aide de formules, mais sinon je le ferait à la main tant pis :dead:

 

[iDanGener]

en entrant les formules dans excel ça doit marcher …

Bonjour,
C’est sarcastique ?

Cependant je dois bien constituer 66 binômes et non 33 : en effet, les 66 élèves doivent envoyer une lettre à un seule élève.
C'est à dire que l'élève A doit envoyer une lettre à B et l'élève B doit envoyer une lettre à C, ainsi de suite...

Bonjour,
Si vous pouviez formuler plus clairement votre problème ce serait plus motivant de chercher une solution.

Si A envoie une lettre à B, est-ce que B peut envoyer une lettre à A ? Si oui, la solution de @radioman est adéquate.

 

[NinaB]

Si A envoie une lettre à B, est-ce que B peut envoyer une lettre à A ? Si oui, la solution de @radioman est adéquate.

L'idéal serait que non.
J'aimerais que A envoie une lettre à B et que B envoie une lettre à C (et je ne veux pas que B envoie une lettre à A).

Je ne sais pas comment être plus claire

 

[iDanGener]

Re-bonjour,
Alors peut-être que ce qui suit pourrait convenir :
Créer 33 binômes (X, Y) comme l’a indiqué @radioman (et précisé par @Aliboron ) où X envoie une lettre à Y, puis créer les 33 binômes correspondants (Y, X+), où Y envoie une lettre au suivant de X dans la liste (à ajuster, lorsqu’on arrive au dernier de la liste).

 

[NinaB]

Merci, je vais essayer en faisant comme cela. Mais il ne risque pas d'y avoir des doublons ?

 

[iDanGener]

Merci, je vais essayer en faisant comme cela. Mais il ne risque pas d'y avoir des doublons ?

Voici à quoi ça pourrait ressembler.

Les 26 + 16 + 24 étudiants des groupes A B et C peuvent s'échanger 66 lettres de la façon présentée dans le tableau joint et que l'on peut lire, pour chaque ligne, X > Y > X+ ((j'utilise le symbole > pour «envoie une lettres à»).

Les quelques premiers et derniers échanges pourraient donc être

A1 > B1 > A2 > B2 > A3 > B3 > A4 > ... > B15 > C23 > B16 > C24 > A1.


​

 

[NinaB]

Voici à quoi ça pourrait ressembler.

Les 26 + 16 + 24 étudiants des groupes A B et C peuvent s'échanger 66 lettres de la façon présentée dans le tableau joint et que l'on peut lire, pour chaque ligne, X > Y > X+ ((j'utilise le symbole > pour «envoie une lettres à»).

Les quelques premiers et derniers échanges pourraient donc être

A1 > B1 > A2 > B2 > A3 > B3 > A4 > ... > B15 > C23 > B16 > C24 > A1.


Voir la pièce jointe 226585​

Ça me semble être une solution convenable, merci beaucoup pour votre aide !!